Liquidity Pool

Abstract

A liquidity pool is a virtual container of funds deposited (locked) on a smart contract by liquidity providers. In exchange, liquidity providers receive LP tokens representing their share of the pool in proportion to how much liquidity they supplied to the pool.

Context

With standard cryptocurrency exchanges or traditional stock markets, trading is based on the order book model. In this model, buyers and sellers come together and place their orders. To make a transaction, a seller and buyer have to reach an agreement on the price of a transaction. This often results in the seller lowering their price and the buyer raising their bid, and this naturally can create a space of misunderstanding and disagreement.

One way to avoid this kind of situation is by engaging market makers, who are always willing to buy or sell assets. With market makers, liquidity can be provided to the market, and users can always make trades without having to wait for different offers to come.

Unfortunately, implementing this solution into the decentralized world won’t work so well because it would be slow, expensive, and unpleasant to the users. The need for something more fitting to this issue brought liquidity pools to life.

Setting up a pool

A Liquidity Pool in its most basic form holds two tokens and each pool creates a new market for that particular pair of tokens. Within yield.vote, we use FVT/ETH paired token pools.

When a pool is created, the balance of both tokens are 0. For the pool to begin working, someone has to seed a pool with an initial deposit for each token. This someone is the first provider, who sets initial price of the pool and initial ratio between tokens.

Let’s see an example:

Example

Carl wants to deposit funds into the ETH/FVT pool. The market algorithm obligates that both values of tokens must be equal. Carl then provides 1 ETH worth 1000 USD and 1000 FVT worth 1000 USD for a total value of 2000 USD.

Carl was providing liquidity into a pool that already existed, and even though he wasn’t the one who made the initial deposit, he still had to follow the rule of providing equal token values into the pool.

Yes, we know that what are you thinking right now is: but why?

The initial price of deposit tokens is set in the moment of setting. That means the ratio between FVT and ETH is taken from current global market price. Obviously, because prices there are dynamic, the value of ETH or FVT will certainly change by the next day, hour, or even minute which creates an arbitrage opportunity.

Example

Let’s stay with Carl a little longer. He provided liquidity into the pool but now the market price of ETH has changed, which created an arbitrage opportunity. Because of that, arbitrage traders will buy ETH in exchange for FVT until the pool ratio reflects the current market price.

Note

Remember that the ratio of the pool changes through LP deposits or trades, and is strictly connected to the amount of tokens in the pool. Also, the pool ratio determines the price of the assets in the pool.

You are probably wondering why a user would need to put both tokens into a pool?

To provide liquidity in a pool, there must be enough of both tokens present. That is ensured by a constant product maker algorithm. The formula is depicted below:

x, y - reserves of tokens A and B

k - constant

Thank to this mathematical check, we can be sure that a pool can always provide liquidity regardless of how large a trade is. The main reason for this is that the algorithm asymptotically increases the price of the token as the desired quantity increases. Trying to buy all the tokens from the pool then a tremendous, and to be honest, impossible task.

Imagine you would like to withdraw ETH from the pool. Let’s say this would be token A. When you take out of the pool some amount of one token, the balance breaks and the constant k changes. To prevent that, you would have to put some FVT (token B) into the pool to the maintain balance. As parameter x changes, y changes as well.

It’s worth mentioning that the k parameter will change anyways due to transaction fees. This has a small impact on the k value, but this shouldn’t concern the user since the k parameter needs to be maintained before fees.

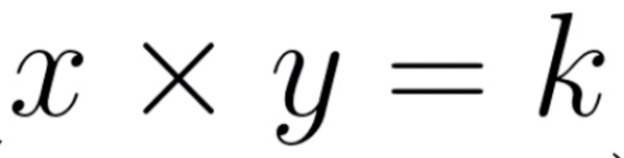
Liquidity Pool Tokens

As mentioned in the beginning, liquidity providers receive LP tokens representing their share in a pool in proportion to how much liquidity they supplied to the pool.

To encourage users to become liquidity providers, every pool charges transaction fee on trades using the liquidity provided that is distributed to LPs upon completion of a trade. Fees vary depending on the pool, but the principle remains the same that transaction fees are distributed proportionally to all LP token holders in the pool.

Since LP tokens are themselves tradable assets, their holders may sell, transfer, or use them in any other way they see fit.

In purpose of retrieving underlying liquidity (plus any fees accrued), users must “burn” their liquidity.

Price impact

As the ratio of tokens in a pool dictates the prices of assets, then buying ETH from the pool will decrease amount of it in the pool, while increasing the amount of FVT in the pool. This transaction would then reflect in the prices of ETH and FVT.

The current market price in a pool only shows the marginal token price, while in practice, a trader buys or sells more than one token at once. And, as the ratio of tokens dictates prices, every token taken out or put into the pool will affect the price of the other token.

This difference between the current market price and the execution price is called price impact. The change of prices depends on the size of the trade in proportion to the size of the pool. The bigger the pool is, the lesser the price impact is.

Price impact is a function of the trade size relative to the liquidity pool size.

Note

It’s worth mentioning that large (or deeper) pools can handle bigger trades without significant price impacts.

Example

Imagine you want to buy 3 apples. You go to the local fruit market and there are only two farmers. Because you are a mathematic maniac, you want the product of <fruit amount> and <money farmer has on hand> to be constant. You also want to pay as little as possible.

1. The first farmer has 5 apples and 10$ on hand. So the constant would be 5 * 10 = 50

   1. You take 3 apples: 5 - 3 = 2

   2. To keep the constant: 50 = (5 - 3) * x

   3. x = 25

   4. So you have to add to farmer hand 15$ (he had 10$ in the beginning, 10 + 15 = 25) to keep the constant on the initial level.

2. second farmer has 78 apples and 100$ in the hand. So constant would be 78 * 100 = 7800

   1. You take 3 apples: 78 - 3 = 75

   2. To keep the constant: 7800 = (78 - 3) * x

   3. x = 104

   4. So you have to add to farmer hand 4$ to keep constant on the initial level.

So the best deal is to buy apples from the second farmer, because to keep the constant on the initial level, you would only have to pay 4$ for 3 apples, while with the first farmer it was 15$.

But let’s stay a little longer on this to clear up price issue. We keep rule of constant alive (price increases as apples amount decreases).

First farmer has 5 apples and 10$ in the hand. If we calculate price of the first apple simply dividing 10$ / 5, then we got 2$, which would be wrong, since 4 * 12$ = 48 while we need to keep the constant on the same level, which is 50. However, that is actually the way of calculating a ratio between apples and dollars, so that makes it a market price.

Anyway, we need to calculate as we did before: (50 / (5 - 1)) - 10$ = 2,5$, and that is the execution price of the first apple, which means that is exactly what you will have to pay.

Out of that we can simply calculate, that price impact is 25%, because 2,5$ is 25% higher than 2$.

Let’s do the same for the second farmer. Market price is a ratio between apples and dollars, so 100$/78 = 1,2821$

But as we calculate execution price, we got (7800/ (78-1)) - 100$ = 1,2987$

Price impact in this case is 1,2948%.